一、线性代数
1、对于向量,若a是标量,为a的绝对值乘以b的向量长度。
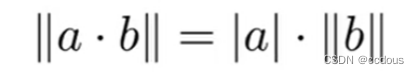
2、点乘
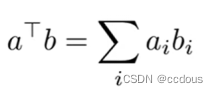
3、范数:向量或者矩阵的长度
L1范数:(对向量)每个元素的绝对值求和
L2范数:(对向量)torch.norm(向量),得到一个标量,元素平方和的开根
F范数:(对矩阵)第4点中
4、范数,b、c为向量,A为矩阵。矩阵范数有点复杂,我们一般用F范数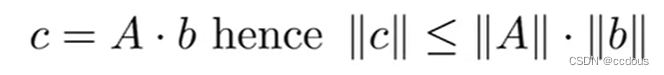
(1)矩阵范数:最小满足上面公式的值
(2)F范数:就像拉长了一样

5、对称和反对称,定义跟线代不太一样,反对称是另一半为负对称
6、正定矩阵:这个矩阵这样乘以任何一个向量都大于等于0
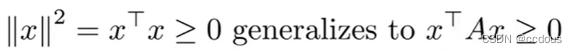
7、正交矩阵

8、置换矩阵(是正交矩阵,每行每列只有一个为1,线代里面我们用于做初等变化)
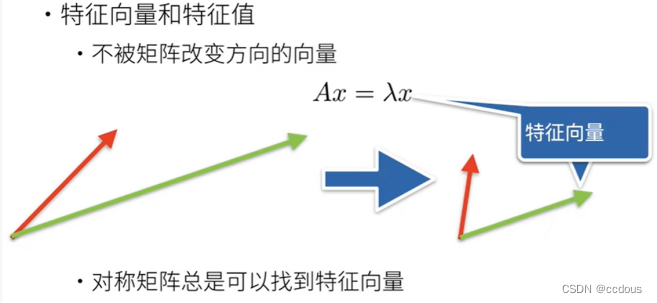
9、特征值与特征向量
二、Pytorch中的线代
1、只有一个元素的张量是标量
2、求和,可以选择轴,降低维度相当于在那个轴上拍扁。
(1)eg: A.shape->torch.Size([2,5,4])
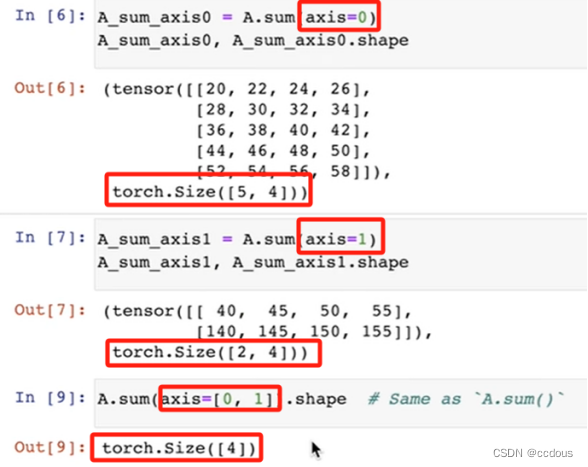
(2)使用keepdims可以保留维度,便于广播机制同样shape操作,被求和那个维度大小变为1,也就是前者直接拍扁了,后者会按的长度为1
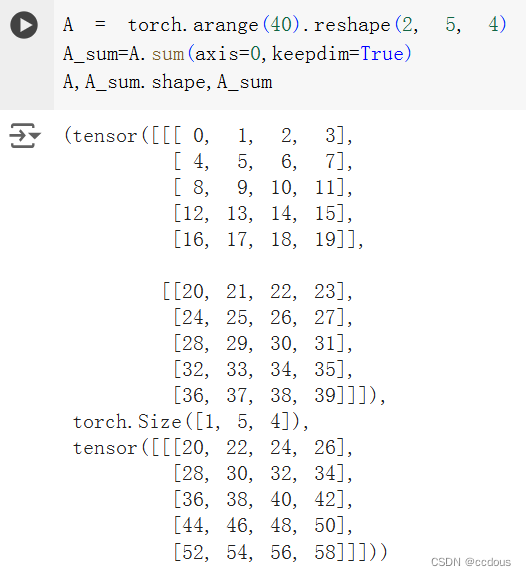
3、求均值A.mean()或A.average(),等价于求和除以元素个数(也可以定维度计算)

此处A.shape[]可得出该维度的长度
4、累加求和A.cumsum(axis=n):每个位置是他前面的元素的和

5、矩阵乘以向量mv=Matrix Vector Multiplication,矩阵乘以矩阵mm

6、求L2范数torch.norm(向量),得到一个标量;求L1范数每个元素的绝对值求和;对矩阵,F范数,前面写到了,torch.norm(矩阵)。
三、矩阵计算
1、亚导数(应用于不可微的函数),比如绝对值函数
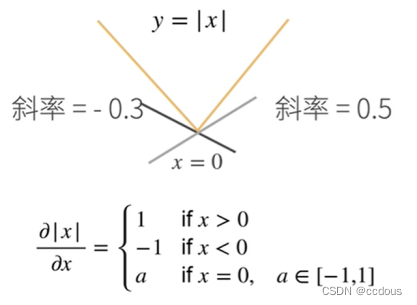
2、将导数扩展到向量则为梯度,表示变化最大的那个方向
(1)Y是标量,x是列向量,y关于x求导是行矩阵


(2)Y是列向量,x是标量,y关于x求导也是列矩阵

(3)向量关于向量求导是矩阵
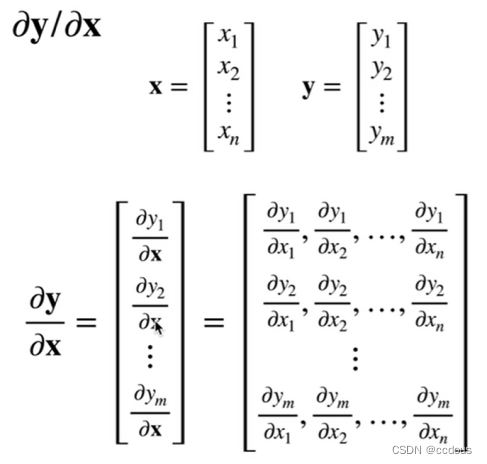
I是对角矩阵,a是与x无关的矩阵

下图中后面部分求导,相当于把下部的向量转置

对不起,李沐老师





![春秋云境:CVE-2022-25411[漏洞复现]](https://img-blog.csdnimg.cn/direct/8927f0354d134f6bad727ffc4ff36c29.png)